Getting started tutorial

[ ]:

%pip install --upgrade --quiet pip
%pip install --upgrade --quiet circuitree==0.11.1 numpy matplotlib tqdm ipympl ffmpeg moviepy watermark

Problem statement

CircuiTree solves the following problem:

Given a phenotype that can be simulated, a reward function that measures the phenotype, and a space of possible circuit architectures, find the optimal architecture(s) to achieve that target phenotype by running a reasonable number of simulations.

In order to solve this problem, CircuiTree uses a search algorithm called Monte Carlo tree search (MCTS), borrowed from artificial intelligence and reinforcement learning, to search over the space of possible architectures, or topologies. MCTS is an algorithm for planning and game-playing, so we approach circuit design as a game of stepwise assembly, where each step adds an interaction to the circuit diagram.

The main class provided by this package is CircuiTree, and to run a tree search, the user should make their own subclass of CircuiTree that defines (1) a space of possible topologies to search and (2) a reward function that returns a (possibly stochastic) estimate of phenotypic quality.

Creating a CircuiTree class

[2]:

from circuitree import CircuiTree

Let’s consider a simple example. Say we are interested in constructing a circuit of three transcription factors (TFs) A, B, and C that exhibits bistability, where the system can be “switched” from one state (e.g. high A, low B) to another (high B, low A). We will allow each TF to activate or inhibit any of the TFs (including itself). Multiple regulation (A both activates and inhibits B) is not allowed. With these rules, we have defined a set of topologies (a design space) that we are sampling from.

[3]:

components = ["A", "B", "C"] # Three transcription factors (TFs)
interactions = [
    "activates", # Each pairwise interaction has two options
    "inhibits",
]

CircuiTree explores the design space by treating circuit design as a game where the topology is built step-by-step, and the objective is to assemble the best circuit. Specifically, CircuiTree represents each circuit topology as a string called a state, and it can choose from a list of actions that either change the state or terminate the assembly process (i.e. “click submit” on the game). The algorithm searches starting from a “root” state, and over many iterations it builds a decision tree of candidate topologies and preferentially explores regions of that tree with higher mean reward.

1. Choose a Grammar

The rules for how states are defined and how they are affected by taking actions (i.e. the rules of the game) are called a “grammar.” We will be using the built-in SimpleNetworkGrammar class to explore the design space we defined above. (See the grammar tutorial for more details on grammars and how to define custom design spaces from the base CircuitGrammar class.)

[4]:

# Built-in grammars can be found in the `models` module
from circuitree.models import SimpleNetworkGrammar

grammar = SimpleNetworkGrammar(
    components=components,
    interactions=interactions,
)

2. Define a reward function

The only strict requirement for the reward function is that it should return bounded values, ideally between 0 and 1. NOTE: If reward values have a larger range, you may need to increase the exploration_constant argument proportionally.

For our test case, bistability is known to require positive feedback. For example, positive autoregulation (A activates itself) or mutual inhibition (A inhibits B and B inhibits A). Here we will use a dummy reward function that doesn’t actually compute bistability but instead just looks for the presence of positive feedback loops. The reward value will be a random number drawn from a Gaussian distribution, and we will increase the mean of that distribution for every type of positive feedback loop the topology contains. In a real scenario, the reward function might be more complex, possibly requiring multiple simulations. To mimic the computational cost of a costly evaluation, we’ll introduce an optional argument expensive that pauses for 0.1 seconds before returning the result.

[5]:

from time import sleep
import numpy as np

def get_bistability_reward(state, grammar, rg=None, expensive=False):
    """Returns a reward value for the given state (topology) based on
    whether it contains positive-feedback loops (PFLs). Assumes the
    state is a string in the format of SimpleNetworkGrammar."""

    # We list all types of PFLs with up to 3 components. Each three-letter
    # substring is an interaction in the circuit, and interactions are
    # separated by underscores.
    patterns = [
        "AAa",  # PAR - "AAa" means "A activates A"
        "ABi_BAi",  # Mutual inhibition - "A inhibits B, B inhibits A"
        "ABa_BAa",  # Mutual activation
        "ABa_BCa_CAa",  # Cycle of all activation
        "ABa_BCi_CAi",  # Cycle with two inhibitions
    ]

    # Mean reward increases with each PFL found (from 0.25 to 0.75)
    mean = 0.25
    for pattern in patterns:

        # The "has_pattern" method returns whether state contains the pattern.
        # It checks all possible renamings. For example, `has_pattern(s, 'AAa')`
        # checks whether the state `s` contains 'AAa', 'BBa', or 'CCa'.
        if grammar.has_pattern(state, pattern):
            mean += 0.1

    if expensive: # Simulate a more expensive reward calculation
        sleep(0.1)

    # Use the default random number generator if none is provided
    rg = np.random.default_rng() if rg is None else rg

    return rg.normal(loc=mean, scale=0.1)

3. Create a subclass

Our subclass of CircuiTree must define the get_reward method. The first argument of the method should be a state, or unique identifier corresponding to a topology. For many features, the method is_success should also be defined. It should take the name of a terminal topology and return True if it is considered “successful” overall at generating the phenotype.

We will say that a successfully bistable circuit should have a mean reward of >0.5, which we will calculate empirically as the cumulative reward divided by the number of samples, or “visits” to that state.

[6]:

class BistabilityTree(CircuiTree):
    """A subclass of CircuiTree that searches for positive feedback networks.
    Uses the SimpleNetworkGrammar to encode network topologies. The grammar can
    be accessed with the `self.grammar` attribute."""

    def __init__(self, *args, **kwargs):
        kwargs = kwargs | {"grammar": grammar}
        super().__init__(*args, **kwargs)

    def get_reward(self, state: str, expensive: bool = False) -> float:
        """Returns a reward value for the given state (topology) based on
        whether it contains positive-feedback loops (PFLs)."""

        # `self.rg` is a Numpy random generator that can be seeded on initialization
        reward = get_bistability_reward(
            state, self.grammar, self.rg, expensive=expensive
        )
        return reward

    def get_mean_reward(self, state: str) -> float:
        """Returns the mean empirical reward value for the given state."""
        # The search graph is stored as a `networkx.DiGraph` in the `graph`
        # attribute. We can access the cumulative reward and # of visits for
        # each node (state) using the `reward` and `visits` attributes.
        return (
          self.graph.nodes[state].get("reward", 0)
          / self.graph.nodes[state].get("visits", 1)
        )

    def is_success(self, state: str) -> bool:
        """Returns whether a topology is a successful bistable circuit design."""
        if self.grammar.is_terminal(state):
            return self.get_mean_reward(state) > 0.5
        else:
            return False # Ignore incomplete topologies

Visualizing results

The best individual topologies

To get an initial feel for the results, let’s plot the 10 designs with the highest average reward after filtering out the states with 10 or fewer samples.

[8]:

import matplotlib.pyplot as plt
from circuitree.viz import plot_network

%matplotlib inline

# Top 10 designs with at least 10 visits
def robustness(state):
    r = tree.graph.nodes[state].get("reward", 0)
    v = tree.graph.nodes[state].get("visits", 1)
    return r / v

# Recall that only the "terminal" states are fully assembled circuits
states = [s for s in tree.terminal_states if tree.graph.nodes[s]["visits"] > 10]
top_10_states = sorted(states, key=robustness, reverse=True)[:10]

# Plot the top 10
fig = plt.figure(figsize=(12, 5))
plt.suptitle("Top 10 bistable circuits and their robustness")
for i, state in enumerate(top_10_states):
    ax = fig.add_subplot(2, 5, i + 1)

    # The `viz.plot_network()` function plots SimpleNetwork-formatted strings
    plot_network(
        *grammar.parse_genotype(state),
        ax=ax,
        plot_labels=False,
        node_shrink=0.6,
        auto_shrink=0.8,
        offset=0.75,
        padding=0.4
    )
    r = tree.graph.nodes[state]["reward"]
    v = tree.graph.nodes[state]["visits"]
    ax.set_title(f"{r / v:.2f} (n={v})")
    ax.set_xlim(-1.5, 1.5)
    ax.set_ylim(-1.0, 1.8)
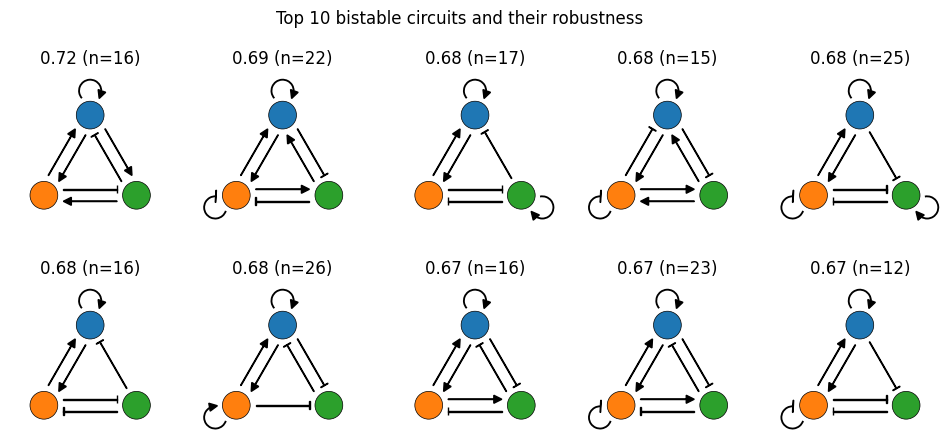
../_images/getting_started_tutorial_1_getting_started_16_0.png

Recall that our reward function is counting the number of different positive feedback loops. By that standard, our best solutions are great! Most contain 3 or 4 different PFLs.

Overall sampling of the search graph

To visualize where the search allocated its samples over the whole search space, we can view the whole search graph at once using a complexity layout.

[9]:

from circuitree.viz import plot_complexity

# Plotting options
plot_kwargs = dict(
    tree=tree,
    aspect=1.5,
    alpha=0.25,
    n_to_highlight=10,  # number of top states to highlight
    highlight_min_visits=10,  # only highlight states with 10+ visits
)
min_visits_per_move = 10

## Plot
fig = plt.figure(figsize=(13, 5))
plt.suptitle("Search space for the Bistability game")

ax1 = fig.add_subplot(1, 2, 1)
plt.title("All moves")
plot_complexity(fig=fig, ax=ax1, **plot_kwargs)

ax2 = fig.add_subplot(1, 2, 2)
plt.title(f"Moves with {min_visits_per_move}+ visits")
plot_complexity(vlim=(min_visits_per_move, None), fig=fig, ax=ax2, **plot_kwargs)

[9]:

(<Figure size 1300x500 with 2 Axes>,
 <Axes: title={'center': 'Moves with 10+ visits'}, ylabel='Complexity'>)
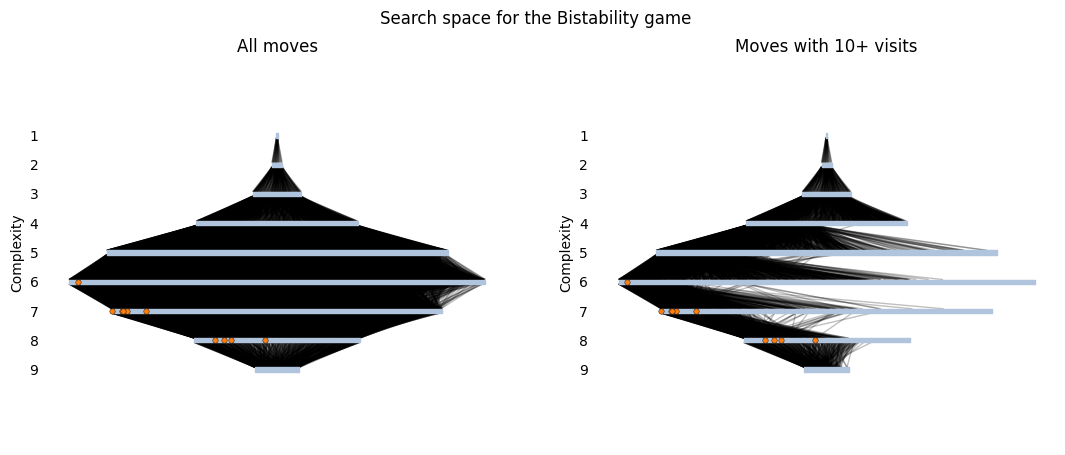
../_images/getting_started_tutorial_1_getting_started_19_1.png

In a complexity layout, terminal topologies are arranged into layers based on their complexity, or the number of interactions in the circuit diagram. The width of the layer represents the number of topologies with that complexity, and topologies within a layer are sorted from most visited to least visited during the search. A line from a less complex topology \(s_i\) to a more complex one \(s_j\) indicates that the assembly move \(s_i \rightarrow s_j\) was visited at least once (left) or at least ten times (right). Finally, we use orange circles to highlight the top 10 topologies shown above.

The graph on the left shows that the overall space is quite well sampled. In all the layers, even the least-visited states (on the right of each layer) have many incoming and outgoing edges, showing that many options were explored. If we only look at the moves with 10+ visits, the graph on the right shows that the search favored a subset of the overall graph that has a higher concentration of top solutions. This is great! It means that our search struck a good balance between exploring the overall space and focusing samples on high-reward areas.